In lockerer Reihenfolge werden wir hier interessante mathematische Sachverhalte „kurz und bündig“ anschaulich erklären. Es geht darum zu zeigen mit welchen Themen Studenten der Mathematik, Physik, Ingenieurwissenschaften und Informatik sich auseinandersetzen müssen. Solche Themen tauchen regelmässig auch in unseren Mathe-Coaching-Lektionen auf, die dann vielschichtig erklärt werden müssen, oft graphisch unterstützend soweit es möglich ist! Uns geht es auch darum, die Schönheit der Mathematik hervorzuheben.
Wir beginnen mit folgendem Beispiel 1:
Die Funktion F(x,y) = sin(x)*sin(y) beschreibt eine Fläche, die über der x-y-Ebene schwebt und durch die Kombination von Sinuswellen in x- und y-Richtung entsteht.
-
mathematiklernen
- Update: 24. Juli 2023
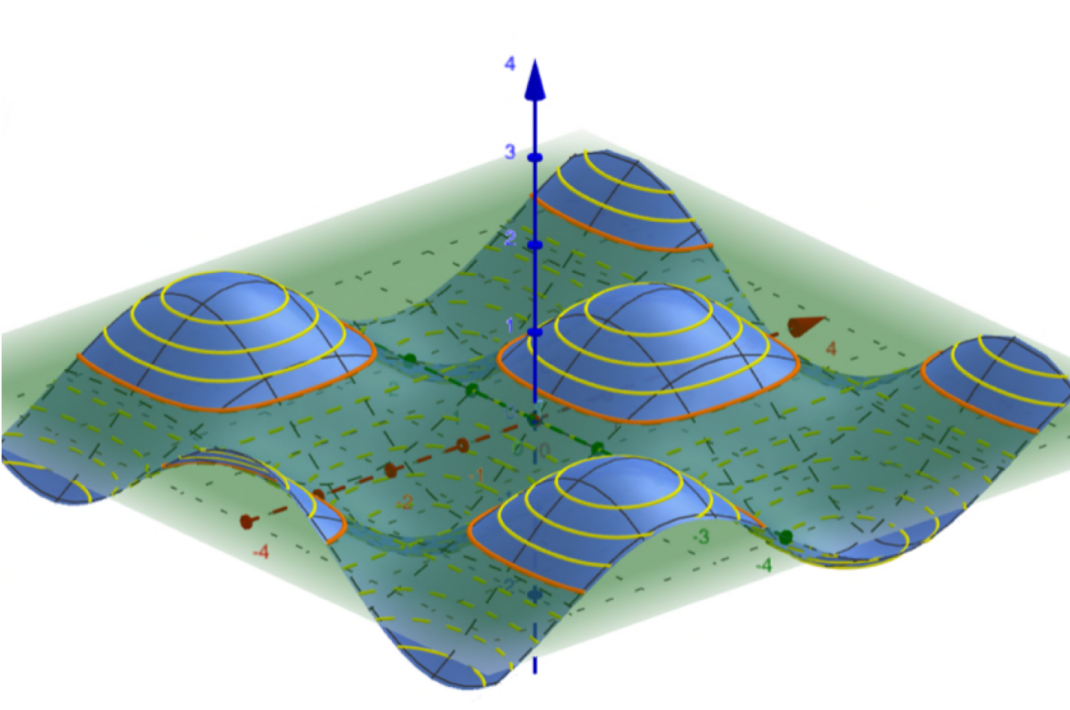
Figure 1: The contour lines are the yellow lines, the section plane is the green plane
- Höhenlinien :
Stellen Sie sich die Höhenlinien des Features wie eine topografische Karte vor. Jede Linie stellt Punkte mit demselben Funktionswert (Höhe) auf der Oberfläche dar. Wenn Sie sich entlang einer dieser Linien bewegen, bleibt die Höhe über dem Boden gleich.
Ähnlich wie beim Wandern auf einem Bergpfad, der auf der gleichen Höhe bleibt. Die Höhenlinien zeigen Ihnen, wie sich die Höhe der Fläche verändert, ohne dass Sie die gesamte dreidimensionale Fläche betrachten müssen.
- Schnittebene parallel zur x-y-Ebene:
Wenn du eine Schnittebene parallel zur x-y-Ebene benutzt, schneidest du buchstäblich einen „Kuchen“ aus der Funktion heraus. Die Höhe dieser Ebene bestimmt, welchen „Teil“ des Kuchens du betrachtest.
Bei unserer Funktion könnte man sich vorstellen, dass die Schnittebene zu einer Höhe passt, die einer bestimmten Höhenlinie entspricht. Du siehst dann nur den Teil der Fläche, der durch diese Schnittebene geschnitten wird, und erhältst eine zweidimensionale Ansicht, die die komplexe Struktur der Funktion auf dieser speziellen Höhe zeigt.
Kombiniert erlauben diese beiden Konzepte eine sehr anschauliche und intuitive Darstellung der komplexen Flächenstruktur, die die Funktion F(x,y) =sin(x)*sin(y) beschreibt.
3. Extrempunkte:
Extrempunkte sind die Gipfel der Berge und die Tiefen der Täler auf unserer Wellenoberfläche. Tatsächlich gibt es in dieser Funktion viele Extrempunkte, da die Sinusfunktion in beiden Richtungen immer wieder ihren höchsten und niedrigsten Wert erreicht.
Die Hochpunkte (Maxima) treten auf, wenn sowohl sin(x) als auch sin(y) einen Wert von 1 haben, und die Tiefpunkte (Minima) treten auf, wenn sie einen Wert von -1 haben. Da die Sinusfunktion periodisch ist, wiederholen sich diese Extrempunkte in regelmäßigen Abständen in beide Richtungen.
Abbildung 2: Die roten Kreise markieren Höhepunkte
Die Kombination aus Höhenlinien und Schnittebenen vermittelt Ihnen ein anschauliches Bild der Berg- und Talstruktur dieses Merkmals und hilft Ihnen, seine komplexen Eigenschaften auf intuitive Weise zu verstehen.
Die Extrempunkte fügen eine weitere Dimension hinzu, indem sie die markanten „Gipfel“ und „Täler“ in dieser Landschaftsdarstellung identifizieren.
Die Funktion F(x,y) = sin(x)*sin(y) mag einfach erscheinen, bietet aber interessante Anwendungen in verschiedenen Bereichen. Zwei Beispiele sollen dies unterstreichen:
1. Welleninterferenz
Diese Funktion kann zur Darstellung der Interferenz von Wellen verwendet werden, wie sie in der Physik oder Ozeanographie auftreten können. Wenn zwei Wellengruppen aufeinandertreffen, beispielsweise in einem Teich oder im Meer, kann die Funktion das resultierende Wellenmuster modellieren.
Die Konturlinien könnten dann die Positionen von Wellenbergen und -tälern im Zeitverlauf zeigen und die Schnittebenen könnten Momentaufnahmen des Wellenmusters zu einem bestimmten Zeitpunkt darstellen..
2. Image processing and computer graphics :
Die Funktion kann auch in der Computergrafik und Bildverarbeitung verwendet werden, um Texturen und Muster zu erstellen. Die wiederkehrenden Wellenberge und -täler des Features können genutzt werden, um realistische Oberflächen wie Sanddünen, Wasseroberflächen oder andere zu erstellen
wiederkehrende Muster zu simulieren. Die Konturlinien könnten die Konturen der Texturen darstellen und die Schnittebenen könnten verwendet werden, um bestimmte Ebenen der Textur in einem 3D-Modell darzustellen .
Diese beiden Beispiele zeigen, dass selbst eine mathematisch einfache Funktion wie F(x,y) = sin(x)*sin(y) nützliche und anschauliche Anwendungen in der realen Welt haben kann. Es hilft uns, Phänomene zu modellieren und zu verstehen, die wir jeden Tag sehen und erleben könnten.
Marcel Liechti
Marcel Liechti, Gehirntrainer GfG, Master of Mathematics UZH. Gründer und Geschäftsführer von mathematik-lernen.ch und begeisterter Mathe Coach. Ich habe an der Universität Zürich und ETH Zürich Mathematik studiert mit den Nebenfächer Informatik und Physik.
Magst du diesen Artikel?
Auf Facebook teilen
Auf Twitter teilien
Auf LinkedIn teilen
Auf Pinterest teilen
Neues Übungsbuch für Bachelor-Studierende 🎓
Verstehe lineare Algebra und komme sicher durch deine Prüfung. 🥇
About
mathematik-lernen.ch ist ein Portal.. Marcel Liechti ist Gründer und Geschäftsführer von mathematik-lernen.ch und begeisterter Mathe Coach. Ich habe an der Universität Zürich und ETH Zürich Mathematik studiert mit den Nebenfächer Informatik und Physik.
Folge uns!
Letzte Artikel
Vorgestellt
Weitere
für dich
interessante Artikel
Mathematik Themen plus viele weitere spannende und wissenswerte Informationen aus anderen themenrelevanten Themen.
Interessante Mathematik Funktionen an Hochschulen
mathematiklernen
24. August 2023
In lockerer Reihenfolge werden wir hier interessante mathematische Sachverhalte „kurz und bündig“ anschaulich erklären. Es geht darum zu zeigen mit welchen Themen Studenten der Mathematik,
Mathe machen, Sudoku oder Kreuzworträtsel lösen, was liebt das Gehirn am meisten?
mathematiklernen
24. August 2023
Marcel Liechti, Mathematik-Coach Die beste „Nahrung“ für das Gehirn ist ein komplexes Zusammenspiel aus Ernährung und mental stimulierenden Aktivitäten. In der Diskussion um geistige Fitness stehen
Was sind die besten Tipps für ein gehirnoptimiertes Lernen für Schüler und Studenten?
mathematiklernen
19. August 2023
Was sind die besten Tipps für ein gehirnoptimiertes Lernen fürSchüler und Studenten? Was sind die besten Tipps für ein gehirnoptimiertes Lernen fürSchüler und Studenten? Mit
JETZT
Kontakt aufnehmen
